Ο διπλασιασμός της περιόδου των λύσεων ενός μη-γραμμικού συστήματος, ως μηχανισμός μετάβασης στις χαοτικές λύσεις, επιδεικνύει την ερμηνευτική του ισχύ. Τα διαγράμματα διακλάδωσης χρησιμοποιούνται για να ερμηνεύσουν την γενικότερη συμπεριφορά του συστήματος, όπως παρουσιάζεται σε άλλο διάγραμμα των παραμέτρων ελέγχου.
Στην ανάρτηση αυτή συνδυάζουμε παλιότερα αποτελέσματα επιχειρώντας να αποκτήσουμε μία γενικότερη εικόνα για την συμπεριφορά του συστήματος. Έτσι, λοιπόν, δεν θα παρουσιάσουμε τίποτα καινούργιο. Ο συνδυασμός όμως των παλιότερων αποτελεσμάτων θα μας εξοπλίσει με μία ισχυρότερη εποπτεία του συστήματος
Ξεκινάμε με την ευαισθησία των αρχικών συνθηκών όπως αυτή αποτυπώνεται στο διάγραμμα του επιπέδου που ορίζεται από τις τιμές δύο παραμέτρων ελέγχου του συστήματος. Το διάγραμμα αυτό παρουσιάζεται στο παρακάτω σχήμα. Ο τρόπος που κατασκευάζεται και άλλες τεχνικές λεπτομέρειες που αφορούν στην "ανάγνωσή" του, στοιχεία της πληροφορίας που περιέχει καθώς επίσης και ορισμένα σχόλια για την δομή του και τα χαρακτηριστικά του, έχουν αποτελέσει αντικείμενο ανάλυσης μιας προηγούμενης ανάρτησης [~]. Το βασικό διάγραμμα που προέκυψε από την εν λόγω ανάλυση παρουσιάζεται στο παρακάτω σχήμα και θα αποτελέσει το σημείο εκκίνησης για περαιτέρω διερεύνηση.
Το διάγραμμα αυτό συνδυάζει τη μεταβολή δύο από τις τρεις παραμέτρους ελέγχου $a,\ b$ και $c$ του συστήματος του Rossler. Διατηρώντας σταθερή την τιμή της $b = 0.8$ και μεταβάλλοντας τις άλλες δύο στα διαστήματα όπου $c\in[4.3,\ 6]$ και $a\in[0.15,\ 0.38]$ λύνουμε αριθμητικά το σύστημα και παίρνουμε την λύση $x(t)$, όπου $t\in [3000, 3700]$, για κάθε ζεύγος τιμών $(a,\ c)$. Tέλος ελέγχουμε την ευαισθησία της λύσης στις αρχικές συνθήκες. Αν η λύση $x(t)$ για το ζεύγος τιμών $(a,\ c)$ εμφανίζει το φαινόμενο της ευαισθησίας τότε αναλόγως με την ένταση που εμφανίζεται αυτό αντιστοιχίζουμε στο σημείο $(a,\ c)$ του διαγράμματος με ένα χρώμα στην κλίμακα του γκρι (με το μαύρο να αντιστοιχεί σε έντονη εμφάνιση του φαινομένου).
Η πληροφορία που περιέχει το διπλανό διάγραμμα είναι αρκετά συμπυκνωμένη και για αυτό είναι ίσως δύσκολο να κατανοήσουμε το ακριβές του περιεχόμενο. Σκοπός της παρούσας ανάλυσης είναι να αποκτήσουμε μία διαισθητική ερμηνεία της εμφάνισης των λευκών και των γκρίζων περιοχών με τη βοήθεια των διαγραμμάτων διακλάδωσης που μας απασχόλησαν σε προηγούμενη ανάρτηση [~].
Η πληροφορία για τη γενικότερη συμπεριφορά του συστήματος είναι πιο άμεση στα διαγράμματα διακλάδωσης, αφού μας δίνεται η ευκαιρία να παρακολουθήσουμε τη συμπεριφορά του συστήματος καθώς μεταβάλλουμε μία μόνο παράμετρο ελέγχου. Επίσης, στα διαγράμματα διακλάδωσης γίνεται φανερή η μετάβαση των λύσεων από τις περιοδικές στις χαοτικές. Είδαμε [~] ότι η μετάβαση αυτή υπαγορεύεται από μία ακολουθία διπλασιασμού της περιόδου των λύσεων, η οποία συνεχίζεται μέχρι το κατώφλι των χαοτικών λύσεων.
Επιχειρώντας να συγκρίνουμε τα δύο αυτά διαγράμματα, ας εστιάσουμε αρχικά την προσοχή μας στον τρόπο με τον οποίο εμφανίζεται το χάος και πως οι χαοτικές λύσεις περιπλέκονται με τις περιοδικές. Για το διάγραμμα των δύο παραμέτρων ελέγχου παρατηρήσαμε μία εξαιρετικά πολύπλοκη εναλλαγή των περιοδικών λύσεων με τις χαοτικές, εστιάζοντας σε διάφορες περιοχές όπου ενώ αρχικά φαίνεται να κυριαρχούν οι χαοτικές λύσεις παρατηρούμε μία λεπτή δομή των λύσεων με "παράθυρα" περιοδικότητας, όπως φαίνεται στο διπλανό "χαμόγελο".
Παρόλο που αυτές οι λεπτοφυείς δομές μας παραπέμπουν σε δομές που μπορούν να σχετίζονται με φαινόμενα αυτοομοιότητας, οι ομοιότητες όσον αφορά στις συγκεκριμένες εναλλαγές περιοδικών και χαοτικών λύσεων με τα διαγράμματα διακλάδωσης είναι πολύ πιο άμεσες. Παρόλο που δεν ασχοληθήκαμε ιδιαίτερα με τις περιοχές των χαοτικών λύσεων στα διαγράμματα διακλάδωσης γίνεται εμφανές ότι υπάρχουν ανάλογα παράθυρα περιοδικής συμπεριφοράς. Προκειμένου να έχουμε μία εικόνα τέτοιων περιοχών, στο παρακάτω διάγραμμα έχει γίνει μία εστίαση του διαγράμματος διακλάδωσης της παραμέτρου $c$ για ένα εύρος τιμών της παραμέτρου, όπου υπάρχουν ως επί το πλείστον χαοτικές λύσεις. Ωστόσο μέσω της εστίασης παρατηρούμε περιοχές όπου οι χαοτικές λύσεις διακόπτονται απότομα και εμφανίζονται καμπύλες και διακλαδώσεις που, αυξάνοντας την τιμή της παραμέτρου, τις θέσεις τους παίρνουν και πάλι χαοτικές λύσεις κ.ο.κ.
Η παρούσα ανάλυση στοχεύει σε μία καλύτερη κατανόηση αυτού του φαινομένου και θα κινηθεί στους δύο τύπους διαγραμμάτων. Στο παραπάνω διάγραμμα οι τιμές της παραμέτρου $c$ βρίσκονται στο διάστημα $[6,\ 6.5]$ και η τιμή της παραμέτρου $a$ διατηρείται σταθερή $a = 0.2$. Για αυτές τις τιμές παρατηρούμε την παρεμβολή δυο περιοχών περιοδικών λύσεων για τις τιμές της παραμέτρου 6.25 περίπου και 6.4. Το μεγάλο διάγραμμα δείχνει πιο λεπτομερώς την γειτονιά της πρώτης περιοχής.
Λαμβάνοντας υπόψη το διάστημα των τιμών της παραμέτρου $c$, στο παραπάνω διάγραμμα καθώς επίσης και την σταθερή τιμή της παραμέτρου $a$ συμπεραίνουμε ότι οι τιμές αυτές βρίσκονται εκτός της περιοχής του διαγράμματος των παραμέτρων για την ευαισθησία στις αρχικές συνθήκες. Στη συνέχεια θα επιχειρήσουμε μία πιο γενική ερμηνεία της συμπεριφοράς του συστήματος, από εκείνη που μας παρέχουν τα διαγράμματα διακλάδωσης, διερευνώντας, μέσω αυτών, το περιεχόμενο του παραπάνω διαγράμματος.
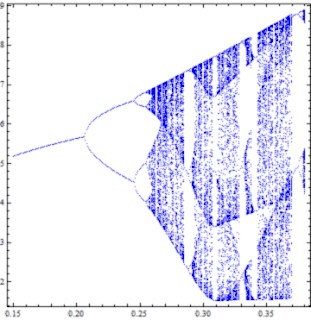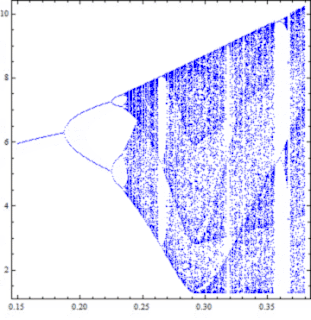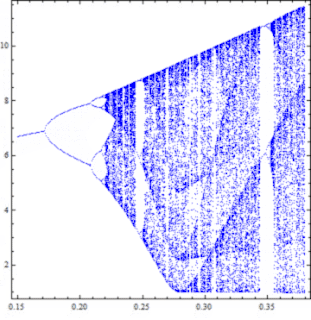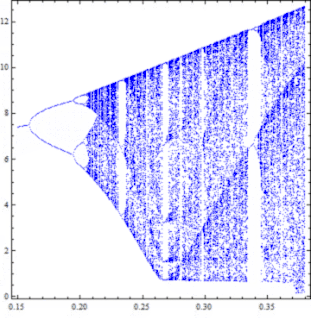
Όπως φαίνεται και στο πρώτο διάγραμμα της ανάρτησης αυτής για μικρές τιμές της παραμέτρου $a$ η συμπεριφορά του συστήματος ξεκινάει με περιοδικές λύσεις, ενώ όσο αυξάνεται σε κάποιο σημείο οι λύσεις αρχίζουν να αποκτούν μία ευαισθησία στις αρχικές συνθήκες, όπου εφαρμόζοντας μία ελάχιστη διαταραχή οι λύσεις αποκλίνουν μεταξύ τους. Σύμφωνα με το διάγραμμα διακλάδωσης της παραμέτρου $a$, στην έκταση της περιοχής των λευκών σημείων για τις μικρές τιμές της παραμέτρου εκτυλίσσεται το φαινόμενο του διπλασιασμού περιόδου των λύσεων, μέχρι που περνάμε στην περιοχή των χαοτικών λύσεων. Αυτή είναι μία γενική συμπεριφορά που όπως φαίνεται και από το γενικό διάγραμμα των παραμέτρων ισχύει για όλες τις τιμές της παραμέτρου $c$. Ας δούμε όμως και πιο ειδικά παραδείγματα.
Επιλέγουμε μία τιμή της παραμέτρου $c$ στον κάθετο άξονα του διαγράμματος. Έστω ότι η τιμή αυτή είναι η $c = 4.7$. Όπως υποδεικνύει το γενικό διάγραμμα υπάρχει ένα διάστημα τιμών της παραμέτρου $a$, όπου εκτυλίσσεται το φαινόμενο διπλασιασμού περιόδου των λύσεων. Το διάστημα αυτό έχει ως δεξί άκρο του λίγο πριν η παράμετρος $a$ αποκτήσει την τιμή $a \approx 0.25$, όπου ξεκινάνε οι χαοτικές λύσεις και όπως φαίνεται και στο σχήμα εκτείνονται στην Α' περιοχή χαοτικών λύσεων. Σύμφωνα πάντα με το σχήμα η περιοχή αυτή θα πρέπει να βρίσκεται χονδρικά στο διάστημα όπου $a\in[0.25,\ 0.27]$. Την περιοχή αυτή διαδέχεται μία ζώνη περιοδικών λύσεων (όπως εκείνη που συναντήσαμε στο προηγούμενο σχήμα παραπάνω), η οποία βρίσκεται γύρω από την τιμή $a =0.27$ (A΄ ζώνη περιοδικών λύσεων). Μετά, για μεγαλύτερες τιμές της παραμέτρου $a$ περνάμε ξανά σε μία περιοχή χαοτικών λύσεων, η οποία διακόπτεται πάλι από μία περιοχή περιοδικών λύσεων (Β' ζώνη περιοδικών λύσεων) περίπου στην τιμή $a = 0.32$. Στη συνέχεια έχουμε μία περιοχή χαοτικών λύσεων και μετά ξανά μία ζώνη περιοδικών λύσεων που αντιστοιχεί στην μεγάλη ζώνη περιοδικότητας που εμφανίζεται στην δεξιά άκρη του διαγράμματος διακλάδωσης. Η σύγκριση των διαγραμμάτων στο διπλανό σχήμα δείχνει ότι οι τιμές αυτές συμπίπτουν αρκετά μεταξύ τους.
Έτσι, αρχίζει να διαφαίνεται μία συσχέτιση της πληροφορίας που περιέχουν οι δύο διαφορετικοί τύποι διαγραμμάτων.
Έτσι, για μία οριζόντια γραμμή, το αριστερό της άκρο ξεκινάει από ένα σημείο της λευκής περιοχής στα αριστερά του διαγράμματος, μέχρι να συναντήσει την αντίστοιχη Α' περιοχή χαοτικών λύσεων η οποία θα διακοπεί από μία λευκή περιοχή, που στο αντίστοιχο διάγραμμα διακλάδωσης θα αντιστοιχεί σε ένα παράθυρο περιοδικών λύσεων, αυτές θα διαδεχτεί μία άλλη περιοχή χαοτικών λύσεων κ.ο.κ. Το διάγραμμα των παραμέτρων μπορεί να μας δώσει τόσο μία ποιοτική, όσο και μία ποσοτική εκτίμηση του διαγράμματος διακλάδωσης της παραμέτρου $a$. Όπως είδαμε και παραπάνω μπορούμε να έχουμε ποσοτικές εκτιμήσεις για τις τιμές της παραμέτρου $a$ που διακόπτεται ο διπλασιασμός των περιόδων ή για εκείνες τις τιμές που εμφανίζονται τα παράθυρα των περιοδικών λύσεων όπως παρεμβάλλονται στις χαοτικές περιοχές.
Για κάθε μία οριζόντια ευθεία (όπως παραπάνω που αντιστοιχεί στην τιμή $c = 4.7$) προκύπτει ένα διάγραμμα διακλάδωσης της παραμέτρου $a$. Βάσει του διαγράμματος των παραμέτρων για την ευαισθησία στις αρχικές συνθήκες, μπορούμε να προβλέψουμε πώς μεταβάλλεται το διάγραμμα διακλάδωσης της $a$ καθώς μεταβάλλεται η $c$. Παρατηρείστε ότι η ακολουθία διπλασιασμού περιόδου τερματίζει για όλο και μικρότερες τιμές της $a$ καθώς αυξάνεται η $c$, ενώ η Α' και η Γ' ζώνη περιοδικών λύσεων ακολουθούν μία "πορεία".
Παρακάτω παρουσιάζεται αυτή η μεταβολή του διαγράμματος διακλάδωσης για την παράμετρο $a$ καθώς αυξάνουμε τη $c$. Ξεκινώντας από την κατώτερη τιμή $c = 4.3$ μέχρι την τιμή $c = 5.77$ και με βήμα $0.01$ κατασκεύασα με το Mathematica 148 διαγράμματα διακλάδωσης προκειμένου να επαληθεύσω τα αποτελέσματα που προέβλεπε το παραπάνω διάγραμμα των παραμέτρων για την ευαισθησία στις αρχικές συνθήκες. Όλα αυτά τα διαγράμματα αν τα προβάλλετε μαζί θα σας δώσουν την αίσθηση μίας συνεχούς μεταβολής, όπου ο διπλασιασμός της περιόδου κινείται προς τα αριστερά, ενώ στις χαοτικές περιοχές εμφανίζονται και εξαφανίζονται παράθυρα περιοδικότητας. Σε επόμενη ανάρτηση θα εστιάσουμε την προσοχή μας και σε άλλες περιοχές, έτσι ώστε να μπορούμε να αναγνώσουμε καλύτερα την πληροφορία που περιέχει το διάγραμμα των παραμέτρων για την ευαισθησία στις αρχικές συνθήκες. Μπορείτε να παρακολουθήσετε τα διαδοχικά διαγράμματα διακλάδωσης κάνοντας αριστερό κλικ στην παρακάτω εικόνα.
______________________________ΣΗΜΕΙΩΣΕΙΣ & ΑΝΑΦΟΡΕΣ
Για να μάθετε περισσότερα σχετικά με το σύστημα Rossler, πατήστε [~].
Για το φαινόμενο της ευαισθησίας στις αρχικές συνθήκες (φαινόμενο της πεταλούδας), πατήστε εδώ [~].
Για το διάγραμμα των παραμέτρων για την ευαισθησία του συστήματος Rossler στις αρχικές συνθήκες , πατήστε εδώ [~].
Για τα διαγράμματα διακλάδωσης των παραμέτρων ελέγχου του συστήματος Rossler, πατήστε εδώ [~].
Το διάγραμμα αυτό συνδυάζει τη μεταβολή δύο από τις τρεις παραμέτρους ελέγχου $a,\ b$ και $c$ του συστήματος του Rossler. Διατηρώντας σταθερή την τιμή της $b = 0.8$ και μεταβάλλοντας τις άλλες δύο στα διαστήματα όπου $c\in[4.3,\ 6]$ και $a\in[0.15,\ 0.38]$ λύνουμε αριθμητικά το σύστημα και παίρνουμε την λύση $x(t)$, όπου $t\in [3000, 3700]$, για κάθε ζεύγος τιμών $(a,\ c)$. Tέλος ελέγχουμε την ευαισθησία της λύσης στις αρχικές συνθήκες. Αν η λύση $x(t)$ για το ζεύγος τιμών $(a,\ c)$ εμφανίζει το φαινόμενο της ευαισθησίας τότε αναλόγως με την ένταση που εμφανίζεται αυτό αντιστοιχίζουμε στο σημείο $(a,\ c)$ του διαγράμματος με ένα χρώμα στην κλίμακα του γκρι (με το μαύρο να αντιστοιχεί σε έντονη εμφάνιση του φαινομένου).
Η πληροφορία που περιέχει το διπλανό διάγραμμα είναι αρκετά συμπυκνωμένη και για αυτό είναι ίσως δύσκολο να κατανοήσουμε το ακριβές του περιεχόμενο. Σκοπός της παρούσας ανάλυσης είναι να αποκτήσουμε μία διαισθητική ερμηνεία της εμφάνισης των λευκών και των γκρίζων περιοχών με τη βοήθεια των διαγραμμάτων διακλάδωσης που μας απασχόλησαν σε προηγούμενη ανάρτηση [~].
Η πληροφορία για τη γενικότερη συμπεριφορά του συστήματος είναι πιο άμεση στα διαγράμματα διακλάδωσης, αφού μας δίνεται η ευκαιρία να παρακολουθήσουμε τη συμπεριφορά του συστήματος καθώς μεταβάλλουμε μία μόνο παράμετρο ελέγχου. Επίσης, στα διαγράμματα διακλάδωσης γίνεται φανερή η μετάβαση των λύσεων από τις περιοδικές στις χαοτικές. Είδαμε [~] ότι η μετάβαση αυτή υπαγορεύεται από μία ακολουθία διπλασιασμού της περιόδου των λύσεων, η οποία συνεχίζεται μέχρι το κατώφλι των χαοτικών λύσεων.
Επιχειρώντας να συγκρίνουμε τα δύο αυτά διαγράμματα, ας εστιάσουμε αρχικά την προσοχή μας στον τρόπο με τον οποίο εμφανίζεται το χάος και πως οι χαοτικές λύσεις περιπλέκονται με τις περιοδικές. Για το διάγραμμα των δύο παραμέτρων ελέγχου παρατηρήσαμε μία εξαιρετικά πολύπλοκη εναλλαγή των περιοδικών λύσεων με τις χαοτικές, εστιάζοντας σε διάφορες περιοχές όπου ενώ αρχικά φαίνεται να κυριαρχούν οι χαοτικές λύσεις παρατηρούμε μία λεπτή δομή των λύσεων με "παράθυρα" περιοδικότητας, όπως φαίνεται στο διπλανό "χαμόγελο".
Παρόλο που αυτές οι λεπτοφυείς δομές μας παραπέμπουν σε δομές που μπορούν να σχετίζονται με φαινόμενα αυτοομοιότητας, οι ομοιότητες όσον αφορά στις συγκεκριμένες εναλλαγές περιοδικών και χαοτικών λύσεων με τα διαγράμματα διακλάδωσης είναι πολύ πιο άμεσες. Παρόλο που δεν ασχοληθήκαμε ιδιαίτερα με τις περιοχές των χαοτικών λύσεων στα διαγράμματα διακλάδωσης γίνεται εμφανές ότι υπάρχουν ανάλογα παράθυρα περιοδικής συμπεριφοράς. Προκειμένου να έχουμε μία εικόνα τέτοιων περιοχών, στο παρακάτω διάγραμμα έχει γίνει μία εστίαση του διαγράμματος διακλάδωσης της παραμέτρου $c$ για ένα εύρος τιμών της παραμέτρου, όπου υπάρχουν ως επί το πλείστον χαοτικές λύσεις. Ωστόσο μέσω της εστίασης παρατηρούμε περιοχές όπου οι χαοτικές λύσεις διακόπτονται απότομα και εμφανίζονται καμπύλες και διακλαδώσεις που, αυξάνοντας την τιμή της παραμέτρου, τις θέσεις τους παίρνουν και πάλι χαοτικές λύσεις κ.ο.κ.
Η παρούσα ανάλυση στοχεύει σε μία καλύτερη κατανόηση αυτού του φαινομένου και θα κινηθεί στους δύο τύπους διαγραμμάτων. Στο παραπάνω διάγραμμα οι τιμές της παραμέτρου $c$ βρίσκονται στο διάστημα $[6,\ 6.5]$ και η τιμή της παραμέτρου $a$ διατηρείται σταθερή $a = 0.2$. Για αυτές τις τιμές παρατηρούμε την παρεμβολή δυο περιοχών περιοδικών λύσεων για τις τιμές της παραμέτρου 6.25 περίπου και 6.4. Το μεγάλο διάγραμμα δείχνει πιο λεπτομερώς την γειτονιά της πρώτης περιοχής.
Λαμβάνοντας υπόψη το διάστημα των τιμών της παραμέτρου $c$, στο παραπάνω διάγραμμα καθώς επίσης και την σταθερή τιμή της παραμέτρου $a$ συμπεραίνουμε ότι οι τιμές αυτές βρίσκονται εκτός της περιοχής του διαγράμματος των παραμέτρων για την ευαισθησία στις αρχικές συνθήκες. Στη συνέχεια θα επιχειρήσουμε μία πιο γενική ερμηνεία της συμπεριφοράς του συστήματος, από εκείνη που μας παρέχουν τα διαγράμματα διακλάδωσης, διερευνώντας, μέσω αυτών, το περιεχόμενο του παραπάνω διαγράμματος.
Όπως φαίνεται και στο πρώτο διάγραμμα της ανάρτησης αυτής για μικρές τιμές της παραμέτρου $a$ η συμπεριφορά του συστήματος ξεκινάει με περιοδικές λύσεις, ενώ όσο αυξάνεται σε κάποιο σημείο οι λύσεις αρχίζουν να αποκτούν μία ευαισθησία στις αρχικές συνθήκες, όπου εφαρμόζοντας μία ελάχιστη διαταραχή οι λύσεις αποκλίνουν μεταξύ τους. Σύμφωνα με το διάγραμμα διακλάδωσης της παραμέτρου $a$, στην έκταση της περιοχής των λευκών σημείων για τις μικρές τιμές της παραμέτρου εκτυλίσσεται το φαινόμενο του διπλασιασμού περιόδου των λύσεων, μέχρι που περνάμε στην περιοχή των χαοτικών λύσεων. Αυτή είναι μία γενική συμπεριφορά που όπως φαίνεται και από το γενικό διάγραμμα των παραμέτρων ισχύει για όλες τις τιμές της παραμέτρου $c$. Ας δούμε όμως και πιο ειδικά παραδείγματα.
Επιλέγουμε μία τιμή της παραμέτρου $c$ στον κάθετο άξονα του διαγράμματος. Έστω ότι η τιμή αυτή είναι η $c = 4.7$. Όπως υποδεικνύει το γενικό διάγραμμα υπάρχει ένα διάστημα τιμών της παραμέτρου $a$, όπου εκτυλίσσεται το φαινόμενο διπλασιασμού περιόδου των λύσεων. Το διάστημα αυτό έχει ως δεξί άκρο του λίγο πριν η παράμετρος $a$ αποκτήσει την τιμή $a \approx 0.25$, όπου ξεκινάνε οι χαοτικές λύσεις και όπως φαίνεται και στο σχήμα εκτείνονται στην Α' περιοχή χαοτικών λύσεων. Σύμφωνα πάντα με το σχήμα η περιοχή αυτή θα πρέπει να βρίσκεται χονδρικά στο διάστημα όπου $a\in[0.25,\ 0.27]$. Την περιοχή αυτή διαδέχεται μία ζώνη περιοδικών λύσεων (όπως εκείνη που συναντήσαμε στο προηγούμενο σχήμα παραπάνω), η οποία βρίσκεται γύρω από την τιμή $a =0.27$ (A΄ ζώνη περιοδικών λύσεων). Μετά, για μεγαλύτερες τιμές της παραμέτρου $a$ περνάμε ξανά σε μία περιοχή χαοτικών λύσεων, η οποία διακόπτεται πάλι από μία περιοχή περιοδικών λύσεων (Β' ζώνη περιοδικών λύσεων) περίπου στην τιμή $a = 0.32$. Στη συνέχεια έχουμε μία περιοχή χαοτικών λύσεων και μετά ξανά μία ζώνη περιοδικών λύσεων που αντιστοιχεί στην μεγάλη ζώνη περιοδικότητας που εμφανίζεται στην δεξιά άκρη του διαγράμματος διακλάδωσης. Η σύγκριση των διαγραμμάτων στο διπλανό σχήμα δείχνει ότι οι τιμές αυτές συμπίπτουν αρκετά μεταξύ τους.
Έτσι, αρχίζει να διαφαίνεται μία συσχέτιση της πληροφορίας που περιέχουν οι δύο διαφορετικοί τύποι διαγραμμάτων.
Έτσι, για μία οριζόντια γραμμή, το αριστερό της άκρο ξεκινάει από ένα σημείο της λευκής περιοχής στα αριστερά του διαγράμματος, μέχρι να συναντήσει την αντίστοιχη Α' περιοχή χαοτικών λύσεων η οποία θα διακοπεί από μία λευκή περιοχή, που στο αντίστοιχο διάγραμμα διακλάδωσης θα αντιστοιχεί σε ένα παράθυρο περιοδικών λύσεων, αυτές θα διαδεχτεί μία άλλη περιοχή χαοτικών λύσεων κ.ο.κ. Το διάγραμμα των παραμέτρων μπορεί να μας δώσει τόσο μία ποιοτική, όσο και μία ποσοτική εκτίμηση του διαγράμματος διακλάδωσης της παραμέτρου $a$. Όπως είδαμε και παραπάνω μπορούμε να έχουμε ποσοτικές εκτιμήσεις για τις τιμές της παραμέτρου $a$ που διακόπτεται ο διπλασιασμός των περιόδων ή για εκείνες τις τιμές που εμφανίζονται τα παράθυρα των περιοδικών λύσεων όπως παρεμβάλλονται στις χαοτικές περιοχές.
Για κάθε μία οριζόντια ευθεία (όπως παραπάνω που αντιστοιχεί στην τιμή $c = 4.7$) προκύπτει ένα διάγραμμα διακλάδωσης της παραμέτρου $a$. Βάσει του διαγράμματος των παραμέτρων για την ευαισθησία στις αρχικές συνθήκες, μπορούμε να προβλέψουμε πώς μεταβάλλεται το διάγραμμα διακλάδωσης της $a$ καθώς μεταβάλλεται η $c$. Παρατηρείστε ότι η ακολουθία διπλασιασμού περιόδου τερματίζει για όλο και μικρότερες τιμές της $a$ καθώς αυξάνεται η $c$, ενώ η Α' και η Γ' ζώνη περιοδικών λύσεων ακολουθούν μία "πορεία".
Παρακάτω παρουσιάζεται αυτή η μεταβολή του διαγράμματος διακλάδωσης για την παράμετρο $a$ καθώς αυξάνουμε τη $c$. Ξεκινώντας από την κατώτερη τιμή $c = 4.3$ μέχρι την τιμή $c = 5.77$ και με βήμα $0.01$ κατασκεύασα με το Mathematica 148 διαγράμματα διακλάδωσης προκειμένου να επαληθεύσω τα αποτελέσματα που προέβλεπε το παραπάνω διάγραμμα των παραμέτρων για την ευαισθησία στις αρχικές συνθήκες. Όλα αυτά τα διαγράμματα αν τα προβάλλετε μαζί θα σας δώσουν την αίσθηση μίας συνεχούς μεταβολής, όπου ο διπλασιασμός της περιόδου κινείται προς τα αριστερά, ενώ στις χαοτικές περιοχές εμφανίζονται και εξαφανίζονται παράθυρα περιοδικότητας. Σε επόμενη ανάρτηση θα εστιάσουμε την προσοχή μας και σε άλλες περιοχές, έτσι ώστε να μπορούμε να αναγνώσουμε καλύτερα την πληροφορία που περιέχει το διάγραμμα των παραμέτρων για την ευαισθησία στις αρχικές συνθήκες. Μπορείτε να παρακολουθήσετε τα διαδοχικά διαγράμματα διακλάδωσης κάνοντας αριστερό κλικ στην παρακάτω εικόνα.
______________________________ΣΗΜΕΙΩΣΕΙΣ & ΑΝΑΦΟΡΕΣ
Για να μάθετε περισσότερα σχετικά με το σύστημα Rossler, πατήστε [~].
Για το φαινόμενο της ευαισθησίας στις αρχικές συνθήκες (φαινόμενο της πεταλούδας), πατήστε εδώ [~].
Για το διάγραμμα των παραμέτρων για την ευαισθησία του συστήματος Rossler στις αρχικές συνθήκες , πατήστε εδώ [~].
Για τα διαγράμματα διακλάδωσης των παραμέτρων ελέγχου του συστήματος Rossler, πατήστε εδώ [~].