Πρώτοι Αριθμοί - Μία πιθανοκρατική θεώρηση (ΙΙ)

Στην ενότητα αυτή θα τιθασεύσουμε την πιθανοκρατική μας προσέγγιση, χρησιμοποιώντας την πανταχού παρούσα λογαριθμική συνάρτηση και μερικά τεχνάσματα που κληρονομήσαμε από τον Newton!

Σε προηγούμενη ανάρτηση [~] βρήκαμε την πιθανότητα ένας δεδομένος ακέραιος $x$ να μη διαιρείται με κανέναν από τους πρώτους $p_{i}$ που είναι μικρότεροί του, δηλαδή για $i$ τέτοιο ώστε $p_{i} < x$. Την πιθανότητα αυτή τη συμβολίζουμε ως $W(x)$ και είδαμε ότι ισούται με

\[
W(x) \approx \prod_{p_{i} \lt x} \Bigl (1 - \frac{1}{p_{i}}\Bigr ).
\]

Πριν προχωρήσουμε κρίνεται αναγκαίο να σχολιάσουμε την παραπάνω έκφραση.

Τα δύο μέλη της έκφασης αυτής δεν συνδέονται με τη σχέση της ισοδυναμίας, αλλά με τη σχέση της κατα προσέγγιση ισοδυναμίας, που τη συμβολίζουμε ως " $\approx$ ". Αυτό συνδέεται άμεσα με την αρχική μας υπόθεση να θεωρήσουμε τις επιμέρους πιθανότητες $\Bigl ( 1 - \frac{1}{p_{i}}\Bigr )$ για κάθε $p_{i}$, ως ανεξάρτητες μεταξύ τους. Το γεγονός αυτό μας επέτρεψε να απλουστεύσουμε κατά πολύ τα πράγματα, αφού έτσι μόνο μπορούμε να πάρουμε το παραπάνω γινόμενο. Ωστόσο, έχουμε πληρώσει το κόστος της απλούστευσης με το να μπορούμε να προσεγγίσουμε την προκείμενη πιθανότητα, χωρίς όμως να μπορούμε να καταλήξουμε σε μία ακριβή αναλυτική έκφραση.

Κατα πόσο είναι καλή είναι αυτή η προσέγγιση;

Πράγματι, τίποτα δεν εγγυάται την ύπαρξη αυτής της ανεξαρτησίας. Δεν υπάρχει κανένα θεώρημα που να δηλώνει ρητά ότι η διαίρεση ενός ακεραίου με έναν συγκεκριμένο πρώτο $p_{i}$, είναι ανεξάρτητη αν ο συγκεκριμένος ακέραιος διαιρείται (ή δεν διαιρείται) με κάποιον άλλον πρώτο $p_{j}$.

Ωστόσο, θα διατηρήσουμε ενεργή αυτή την υπόθεση για να δούμε που μπορεί να καταλήξουμε. Δεδομένου ότι οι δύο ποσότητες είναι θετικές, τις θέτουμε ως ορίσματα της λογαριθμικής συνάρτησης,
\[
\begin{align}
\log{W(x)} &\approx \log{ \prod_{p_{i}\lt x}\Bigl (1 - \frac{1}{p_{i}}\Bigr )}\\
\log{W(x)} &\approx \sum_{p_{i}\lt x} \log{\Bigl ( 1 - \frac{1}{p_{i}}\Bigr )}
\end{align}
\]
Ο βασικός λόγος που γίνεται αυτό είναι να μετατρέψουμε το γινόμενο του δεξιού μέλους της σχέσης σε άθροισμα και η λογαρίθμιση αποτελεί ένα πολύ σύνηθες τέχνασμα. Ας συγκεντρώσουμε την προσοχή μας στην ποσότητα του αθροίσματος. Για μεγάλους πρώτους ισχύει ότι $\frac{1}{p_{i}} \rightarrow 0$ καθώς $p_{i}\rightarrow \infty$. Αυτό σημαίνει ότι η ποσότητα $1 - \frac{1}{p_{i}}$ τείνει στο $1$ και τελικά η $\log{\Bigl (1 - \frac{1}{p_{i}}\Bigr )}$ τείνει στο $0$.

Αυτό φαίνεται και στην παρακάτω γραφική παράσταση της λογαριθμικής συνάρτησης. Στο διάγραμμα αυτό σημειώνεται στον οριζόντιο άξονα η ποσότητα $1-\varepsilon$, όπου η $\varepsilon$ αντιστοιχεί σε μία ποσότητα αρκετά μικρή ώστε η $1-\varepsilon$ να μην ξεφεύγει από την γειτονιά του $1$. Η ποσότητα αυτή μέσω της λογαριθμικής συνάρτησης απεικονίζεται στον κάθετο άξονα σε ένα σημείο κοντά στην περιοχή του $0$ που προσεγγίζεται με την ποσότητα $-\varepsilon$.


Αν θέσουμε όπου $\varepsilon = \frac{1}{x}$ τότε πώς θα συμπεριφέρεται η συνάρτηση $\log{\Bigl (1 - \frac{1}{x}\Bigr )}$ για μεγάλες τιμές του $x$;

Συναφή ερωτήματα απασχολούσαν τους μαθηματικούς από τις πρώτες κιόλας στιγμές της γέννησης του απειροστικού λογισμού. Γνωρίζουμε, για παράδειγμα, ότι ο Isaac Newton (1642 - 1727) καθώς επίσης και ο Nicolas Mercator (1620 - 1687) ανέπτυξαν, ανεξάρτητα ο ένας από τον άλλον, την έκφραση $\frac{1}{(1 + x)}$ σε μία σειρά με άπειρους όρους, αποδεικνύοντας ότι
\[
\frac{1}{1+x} = 1 - x + x^{2} - x^{3} + x^{4} - x^{5} + \ldots
\]
Ολοκληρώνοντας και τα δύο μέλη ως προς $x$ προκύπτει
\[
\log{(1+x)} = x - \frac{1}{2}x^{2} + \frac{1}{3}x^{3} + \ldots
\]
Προσαρμόζοντας τις δύο αυτές ποσότητες στην περίπτωση που εξετάζουμε θέτουμε απλά όπου $x = -\frac{1}{r}$ με $r$ τη νέα μας μεταβλητή. Παρατηρείστε ότι η δεύτερη έκφραση γίνεται
\[
\log{\Bigl (1 - \frac{1}{r}\Bigr )} = -\frac{1}{r} - \frac{1}{2}\Bigl (\frac{1}{r}\Bigr )^{2} - \frac{1}{3}\Bigl (\frac{1}{r}\Bigr )^{3} - \ldots
\]
Για μεγάλες τιμές του $x$ οι τιμές των όρων του δεύτερου μέλους μειώνονται εκθετικά, εκτός από τον πρώτο όρο. Επομένως, μία καλή πρώτη προσέγγιση για την ποοσότητα $\log{\Bigl (1 - \frac{1}{x}\Bigr )}$ είναι η $-\frac{1}{x}$. Για αυτό μπορούμε να γράψουμε $\log{\Bigl ( 1 - \frac{1}{x}\Bigr )} \approx -\frac{1}{x}$. Έτσι, παίρνουμε μία καλή πορσέγγιση, η οποία βελτιώνεται όλο και περισσότερο για μεγάλες τιμές της μεταβλητής, όπως φαίνεται και στην παρακάτω κοινή γραφική παράσταση των συναρτήσεων $-1/x$ και $\log{(1 - 1/x)}$.

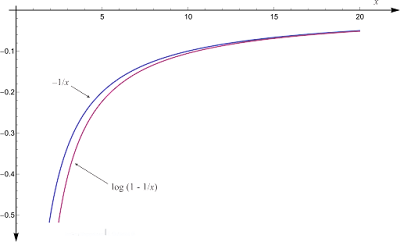Τα αποτελέσματα αυτά θα τα χρησιμοποιήσουμε στην σχέση που καταλήξαμε παραπάνω για την πιθανότητα $W(x)$, ένας ακέραιος $x$ να μην εμφανίζει στο ανάπτυγμα των πρώτων παραγόντων του κανέναν πρώτο $p_{i}$ μικρότερο του $x$. Είδαμε παραπάνω ότι η πιθανότητα αυτή αντιστοιχεί στο γεγονός ο ακέραιος $x$ να είναι πρώτος και καταλήξαμε ότι,
\[
\log{W(x)} \approx \sum_{p_{i}\le x}\log{\Bigl (1 - \frac{1}{p_{i}}\Bigr )}
\]
Σύμφωνα με τα παραπάνω, για μεγάλους πρώτους μπορούμε να γράψουμε
\[
\log{W(x)} \approx -\sum_{p_{i}\le x}\frac{1}{p_{i}}.
\]
Αυτό που έχουμε καταφέρει μέχρι στιγμής είναι να απλουστεύσουμε αρκετά την αρχική έκφραση της πιθανότητας $W(x)$. H έκφραση του αθροίσματος αναφέρεται μόνο στους πρώτους που είναι μικρότεροι από τον δεδομένο αριθμό. Αυτό προϋποθέτει να γνωρίζουμε όλο αυτό το υποσύνολο των πρώτων αριθμών. Άρα, για να υπολογίσουμε την πιθανότητα ένας αριθμός να είναι πρώτος θα πρέπει να γνωρίζουμε όλους τους πρώτους που προηγούνται από αυτόν. Η χρησιμότητα της παραπάνω σχέσης είναι ασήμαντη!

Μην αποθαρρύνεστε όμως... Αυτό θα μας δώσει ώθηση να συνεχίσουμε βελτιώνοντας ακόμη περισσότερο την παραπάνω έκφραση και διερευνώντας μεθόδους που θα την καταστήσουν πιο χρήσιμη!

_________________________________________________________

- Για μία εισαγωγή στους πρώτους αριθμούς [~]

- Η αναρτηση αυτή είναι συνέχεια του πρώτου μέρους. Για το πρώτο μέρος πατήστε εδώ [~]